Nsryjdtyk

Cilindro circolare retto

In matematica un cilindro ellittico è una quadrica (cioè una superficie nello spazio tridimensionale definita da un'equazione polinomiale di secondo grado in x{displaystyle x}, y{displaystyle y}, z{displaystyle z}), che soddisfa la seguente equazione in coordinate cartesiane:

(xa)2+(yb)2=1.{displaystyle left({frac {x}{a}}right)^{2}+left({frac {y}{b}}right)^{2}=1.}

Questa è l'equazione di un cilindro ellittico. Un cilindro può essere anche considerato un prisma a base circolare, dove il numero dei rettangoli è quindi infinito.

Se a=b{displaystyle a=b} si ha la superficie di un cilindro circolare. Il cilindro è una quadrica degenere in quanto una delle coordinate dello spazio non compare nella sua equazione (nel caso precedente la coordinata z{displaystyle z}). Secondo certe terminologie i cilindri non sono considerati casi particolari di quadriche.

Cilindro circolare piano e troncato |

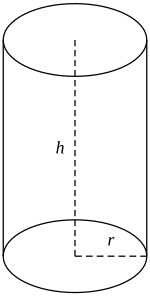
Nell'uso comune, con la parola cilindro si intende l'insieme limitato dei punti delimitati da un cilindro circolare retto e da due piani ortogonali al suo asse; alle sue due estremità piane esso presenta due superfici circolari, come nella figura a destra. Se questo cilindro ha raggio r{displaystyle r} e altezza h{displaystyle h}, il suo volume è dato da

V=πr2h,{displaystyle V=pi r^{2}h,}

e la sua superficie laterale

Al=2πrh,{displaystyle A_{l}=2pi rh,}

mentre la sua superficie totale è data dalla somma della superficie laterale e del doppio della superficie di base.

Superficie di base:

Ab=πr2{displaystyle A_{b},=,pi r^{2}}

Superficie totale:

At=2Ab+Al=2πr2+2πrh{displaystyle A_{t},=,2A_{b}+A_{l}=2pi r^{2}+2pi rh}

Si può calcolare il volume del cilindro per mezzo del calcolo integrale come il volume del solido ottenuto dalla rotazione di una retta parallela all'asse delle ordinate (del tipo y=k{displaystyle y=k}, con k{displaystyle k} costante) attorno all'asse delle ascisse. Si ha:

V=∫0hπk2dx=πr2h.{displaystyle V=int _{0}^{h}pi k^{2}dx=pi r^{2}h.}

Essendo k{displaystyle k} proprio il raggio r{displaystyle r} del cilindro.

Per un dato volume, il cilindro con la minima area superficiale, ha h=2r{displaystyle h=2r}. Per una data area superficiale, il cilindro con più esteso volume ha h=2r{displaystyle h=2r}. Un cilindro di questo tipo è detto cilindro equilatero.

Qualora si dovesse calcolare il volume di un cilindro circolare troncato si deve utilizzare la seguente formula^[1]:

V=πr2(h+H)/2,{displaystyle V=pi r^{2}(h+H)/2,}

dove h{displaystyle h} indica la lunghezza del lato corto, mentre H{displaystyle H} indica la lunghezza del lato lungo.

Nel caso si dovesse calcolare la superficie laterale di un cilindro circolare troncato la formula è:

Al=πr(h+H).{displaystyle A_{l}=pi r(h+H).}

Cilindro ellittico, iperbolico e parabolico^[2] |

Cilindro ellittico

Un cilindro ellittico è invariante per le rotazioni di π{displaystyle pi } intorno al suo asse di simmetria, l'asse delle z{displaystyle z} nel caso della equazione di partenza; esso è anche invariante per tutte le traslazioni dirette come il suo asse. Un cilindro circolare è anche invariante per tutte le rotazioni intorno al suo asse.

Ci sono altri tipi di cilindro meno usuali. Quello caratterizzato dall'equazione che segue viene detto cilindro ellittico immaginario:

(xa)2+(yb)2=−1,{displaystyle left({frac {x}{a}}right)^{2}+left({frac {y}{b}}right)^{2}=-1,}

il cilindro iperbolico ha equazione:

(xa)2−(yb)2=1,{displaystyle left({frac {x}{a}}right)^{2}-left({frac {y}{b}}right)^{2}=1,}

mentre il cilindro parabolico ha equazione:

x2+2y=0.{displaystyle x^{2}+2y=0.}

Più in generale, data una curva ed una retta, un cilindro è la superficie rigata costituita dalle rette parallele alla retta data ed incidenti con la curva.

Il volume di riempimento di cilindro orizzontale |

Un problema ricorrente è il calcolo del volume di liquido posto all'interno di un cilindro in orizzontale di lunghezza L{displaystyle L} e raggio r{displaystyle r}, in funzione dell'altezza h≤2r{displaystyle hleq 2r} raggiunta dal liquido. Il problema è di facile risoluzione: il volume è pari all'area sottesa tra la corda di altezza h{displaystyle h} e la circonferenza, moltiplicata per la lunghezza L{displaystyle L} del cilindro.

Cilindro con h < r

Cilindro con h > r

Sia α{displaystyle alpha } l'angolo al centro (misurato in radianti) che insiste sulla corda; stabiliamo sia 0≤α≤π{displaystyle 0leq alpha leq pi } se 0≤h≤r{displaystyle 0leq hleq r} e π<α≤2π{displaystyle pi <alpha leq 2pi } se invece r<h<2r{displaystyle r<h<2r}; sarà:

sin⁡α2=2rh−h2r{displaystyle sin {frac {alpha }{2}}={frac {sqrt {2rh-h^{2}}}{r}}}

cos⁡α2=r−hr.{displaystyle cos {frac {alpha }{2}}={frac {r-h}{r}}.}

La formula sarà allora data dall'area della sezione circolare individuata dall'angolo α{displaystyle alpha } meno il prodotto

(rcos⁡α2)(rsin⁡α2)=(r−h)2rh−h2,{displaystyle left(rcos {frac {alpha }{2}}right)left(rsin {frac {alpha }{2}}right)=(r-h){sqrt {2rh-h^{2}}},}

(che rappresenta l'area del triangolo che ha come vertici il centro del cerchio e le intersezioni fra i lati dell'angolo e la circonferenza, o il suo opposto, a seconda del segno di r−h{displaystyle r-h}), il tutto moltiplicato per la lunghezza L{displaystyle L} del cilindro, e quindi:

Vh=L(12αr2−(r−h)2rh−h2).{displaystyle V_{h}=Lleft({frac {1}{2}}{alpha r^{2}}-(r-h){sqrt {2rh-h^{2}}}right).}

Dall'applicazione del calcolo integrale si ottiene invece la seguente formula, valida per qualsiasi altezza di liquido (h{displaystyle h}) sia per un livello al di sotto della metà del serbatoio, sia per un livello al di sopra della metà stessa, applicabile misurando direttamente la sola altezza h del liquido e conoscendo la lunghezza del cilindro e il suo raggio. In tale formula, per h{displaystyle h} si intende l'altezza di liquido misurata con l'asticella graduata dal fondo del serbatoio.

Vh=L(r2arccos⁡(r−h)r+(h−r)2hr−h2).{displaystyle V_{h}=Lleft(r^{2}arccos {frac {(r-h)}{r}}+(h-r){sqrt {2hr-h^{2}}}right).}

Va tuttavia tenuto presente che generalmente i serbatoi non sono perfettamente cilindrici. Vengono pertanto predisposte apposite tabelle di ragguaglio per la determinazione del volume di liquido, contenuto in un serbatoio posto orizzontalmente, in base al livello del liquido stesso.

Note |

Voci correlate |

• Quadrica


• Anticlessidra

Altri progetti |

• 
  Wikizionario contiene il lemma di dizionario «cilindro»


• 
  Wikimedia Commons contiene immagini o altri file su cilindro
  

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica