Nsryjdtyk

.mw-parser-output .nota-disambigua{clear:both;margin-bottom:.5em;border:1px solid #CCC;padding-left:4px}.mw-parser-output .nota-disambigua i{vertical-align:middle}

La sfera (dal greco σφαῖρα, sphaîra) è il solido geometrico costituito da tutti i punti che sono a distanza minore o uguale a una distanza fissata r{displaystyle r}, detta raggio della sfera, da un punto O{displaystyle O} detto centro della sfera.

L'insieme dei punti la cui distanza è eguale a r{displaystyle r} è detto superficie sferica di centro O{displaystyle O} e raggio r{displaystyle r}.

È detta "semisfera" ciascuna delle metà di un solido sferico diviso in due da un piano passante per il centro o anche ciascuna delle due superfici di una sfera divisa da una sua circonferenza massima.

Rappresentazione analitica |

In geometria cartesiana, una superficie sferica con centro (x0,y0,z0){displaystyle (x_{0},y_{0},z_{0})} e di raggio r{displaystyle r} è rappresentata dall'insieme di punti (x,y,z){displaystyle (x,y,z)} tali che

(x−x0)2+(y−y0)2+(z−z0)2=r2{displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=r^{2}}

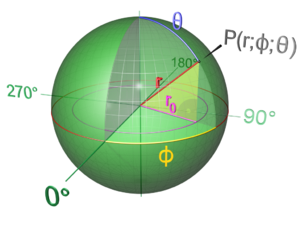
I punti della superficie sferica possono essere parametrizzati in coordinate sferiche nel modo seguente

{x=x0+rsin⁡ϑcos⁡φy=y0+rsin⁡ϑsin⁡φz=z0+rcos⁡ϑ{displaystyle left{{begin{aligned}x&=x_{0}+rsin vartheta cos varphi \y&=y_{0}+rsin vartheta sin varphi \z&=z_{0}+rcos vartheta end{aligned}}right.}

dove ϑ{displaystyle vartheta } e φ{displaystyle varphi } rappresentano la latitudine e la longitudine del punto, variando negli intervalli

0≤ϑ≤π,−π≤φ<π.{displaystyle 0leq vartheta leq pi ,quad -pi leq varphi <pi .}

Ogni punto della superficie sferica è descritto da una sola coppia (ϑ,φ){displaystyle (vartheta ,varphi )} di questo tipo, tranne i poli: la coppia (0,φ){displaystyle (0,varphi )} descrive sempre il polo nord, e (π,φ){displaystyle (pi ,varphi )} sempre il polo sud (per qualsiasi valore di φ{displaystyle varphi }).

Alternativamente si può utilizzare l'equazione cartesiana della superficie sferica:

x2+y2+z2+ax+by+cz+d=0{displaystyle x^{2}+y^{2}+z^{2}+ax+by+cz+d=0}

con a{displaystyle a}, b{displaystyle b}, c{displaystyle c}, d{displaystyle d}, numeri reali tali che a2+b2+c2−4d>0{displaystyle a^{2}+b^{2}+c^{2}-4d>0}. Dall'equazione cartesiana si possono ricavare le coordinate del centro:

C(−a2;−b2;−c2).{displaystyle Cleft(-{dfrac {a}{2}};-{dfrac {b}{2}};-{dfrac {c}{2}}right).}

Superficie |

L'area della superficie di una sfera di raggio R{displaystyle R} è data dall'equazione:

A=4πR2.{displaystyle A=4pi R^{2}.}

Dimostrazione analitica in coordinate cartesiane |

La sfera può essere pensata come un solido di rotazione ottenuto ruotando attorno all'asse x{displaystyle x} il grafico della funzione

f(x)=R2−x2,{displaystyle f(x)={sqrt {R^{2}-x^{2}}},}

che rappresenta una semicirconferenza di raggio R{displaystyle R}. Pertanto, per il primo teorema di Guldino, la superficie laterale è data da:

A=2π∫−R+Rf(x)1+[f′(x)]2dx=2π∫−R+RR2−x2RR2−x2dx=2π∫−R+RRdx=2πR(R+R)=4πR2.{displaystyle A=2pi int _{-R}^{+R}f(x){sqrt {1+[f'(x)]^{2}}},dx=2pi int _{-R}^{+R}{sqrt {R^{2}-x^{2}}}{frac {R}{sqrt {R^{2}-x^{2}}}},dx=2pi int _{-R}^{+R}R,dx=2pi R(R+R)=4pi R^{2}.}

Dimostrazione analitica in coordinate polari |

La superficie totale della sfera si può ottenere, per il primo teorema di Guldino, tramite il seguente integrale:

A=2π∫0πR2sin⁡ϑdϑ=2πR2(−cos⁡π+cos⁡0)=4πR2.{displaystyle A=2pi int _{0}^{pi }R^{2}sin vartheta ,dvartheta =2pi R^{2}(-cos pi +cos 0)=4pi R^{2}.}

Volume |

Il volume della sfera di raggio R{displaystyle R} è dato dall'equazione (integrale in dR{displaystyle dR} della superficie):

V=AR3=4πR33{displaystyle V={frac {AR}{3}}={frac {4pi R^{3}}{3}}}

La dimostrazione di questa formula può essere ottenuta in modo immediato usando il metodo degli indivisibili oppure con gli strumenti nell'analisi matematica.

Dimostrazione analitica |

Si pensi di sommare tutte le aree dei cerchi che si ottengono sezionando la sfera con dei piani orizzontali. Il raggio di questi cerchi varierà con una funzione f(l){displaystyle f(l)} della distanza del piano orizzontale dal centro della sfera e dato che l'area di un cerchio equivale a π{displaystyle pi } per il raggio al quadrato:

V=∫−R+Rπf2(l)dl{displaystyle V=int _{-R}^{+R}pi f^{2}(l),dl}

dove l{displaystyle l} appunto è la distanza del piano dal centro della sfera.

Raggio alla distanza x{displaystyle x}

s=r2−x2{displaystyle s={sqrt {r^{2}-x^{2}}}}

Dunque, dal teorema di Pitagora, f(l){displaystyle f(l)} vale:

f(l)=R2−l2{displaystyle f(l)={sqrt {R^{2}-l^{2}}}}

che, sostituita nell'equazione del volume, si trova:

V=∫−R+Rπ(R2−l2)dl=π∫−R+RR2dl−π∫−R+Rl2dl=2πR3−23πR3=43πR3.{displaystyle V=int _{-R}^{+R}pi (R^{2}-l^{2}),dl=pi int _{-R}^{+R}R^{2},dl-pi int _{-R}^{+R}l^{2},dl=2pi R^{3}-{frac {2}{3}}pi R^{3}={frac {4}{3}}pi R^{3}.}

Allo stesso modo si può calcolare il volume VKS{displaystyle V_{mathrm {KS} }} di un segmento di sfera di altezza h{displaystyle h}

VKS=∫r−hrAxdx=r2π[x]r−hr−13π[x3]r−hr{displaystyle V_{mathrm {KS} }=int _{r-h}^{r}{A_{x}dx}=r^{2}pi left[xright]_{r-h}^{r}-{1 over 3}pi left[{x^{3}}right]_{r-h}^{r}}

VKS=r2π[r−(r−h)]−13π[r3−(r−h)3]=πr2h−13π[r3−(r3−3r2h+3rh2−h3)]{displaystyle V_{mathrm {KS} }=r^{2}pi left[r-(r-h)right]-{1 over 3}pi left[r^{3}-(r-h)^{3}right]=pi r^{2}h-{frac {1}{3}}pi left[r^{3}-(r^{3}-3r^{2}h+3rh^{2}-h^{3})right]}

VKS=πr2h−πr2h+πrh2−13πh3=πh23(3r−h){displaystyle V_{mathrm {KS} }=pi r^{2}h-pi r^{2}h+pi rh^{2}-{1 over 3}pi h^{3}={pi h^{2} over 3}(3r-h)}

Dimostrazione tramite infinitesimi |

La sfera può anche essere intesa come l'insieme di numerose piramidi infinitesime, tutte con il vertice nel centro della sfera e con i poligoni di base delle piramidi che poggiano sulla superficie della sfera: queste infinite piramidi elementari riempiranno tutto e solo il volume della sfera. Il volume di ogni piramide è:

area di base⋅altezza3{displaystyle {frac {{mbox{area di base}}cdot {mbox{altezza}}}{3}}}

dal quale si desume il significato della formula per il volume della sfera.

Altre proprietà |

La sfera è la figura tridimensionale con il minimo rapporto superficie/volume: ciò spiega perché a tale forma tendono molti oggetti fisici, dalle gocce di liquido ai corpi celesti. Ad esempio, le bolle sono sferiche perché la tensione superficiale tende a minimizzare l'area a parità di volume.

Il cilindro circoscritto ha un volume che è 3/2{displaystyle 3/2} quello della sfera, ed una superficie laterale che è la stessa di quella della sfera. Questo fatto, e le formule scritte sopra, erano già noti ad Archimede.

Con l'aumentare del raggio, il volume della sfera cresce più della superficie. Infatti il rapporto fra queste due quantità è R/3{displaystyle R/3}.

Una sfera può anche essere definita come formata da un semicerchio che ruota intorno al suo diametro. Se si usa una ellisse, si ottiene un ellissoide di rotazione.

Terminologia |

Due punti della superficie sferica che stanno sulla stessa retta passante per l'origine sono detti antipodali, e una tale retta è detta asse, poiché è un asse di simmetria della sfera.

Un cerchio massimo è una circonferenza avente lo stesso centro della sfera, ottenuta quindi intersecando la superficie sferica con un piano passante per l'origine.

Se un punto della superficie sferica è identificato come polo nord, il suo antipodale è il polo sud e l'equatore è il cerchio massimo equidistante dai due poli. I cerchi massimi passanti per i poli sono i meridiani, mentre la linea retta passante per l'origine ed i due poli è l'asse. Questa terminologia è usata anche per i corpi celesti come la terra, anche se non perfettamente sferici.

Generalizzazioni ad altre dimensioni |

La sfera può essere generalizzata in altre dimensioni. Per ogni numero naturale n{displaystyle n}, una sfera n{displaystyle n}-dimensionale è l'insieme dei punti nello spazio euclideo (n+1){displaystyle (n+1)}-dimensionale Rn+1{displaystyle mathbb {R} ^{n+1}} che hanno una distanza fissata r>0{displaystyle r>0} da un certo punto dello spazio.

Ad esempio:

• una sfera 0-dimensionale è fatta di una coppia di punti {−r,r}{displaystyle {-r,r}} in R{displaystyle mathbb {R} };


• una sfera 1-dimensionale è una circonferenza di raggio r{displaystyle r} nel piano;


• una sfera 2-dimensionale è la superficie sferica ordinaria;


• una sfera 3-dimensionale è una sfera nello spazio Euclideo 4-dimensionale.

Le sfere di dimensione > 2 sono chiamate anche ipersfere. La sfera n{displaystyle n}-dimensionale di raggio unitario, centrata nell'origine, viene indicata con Sn{displaystyle S^{n}}.

Generalizzazioni in spazi metrici |

Più in generale, in uno spazio metrico (E,d){displaystyle (E,d)}, la sfera di centro x{displaystyle x} e raggio r>0{displaystyle r>0} è l'insieme

S(x;r)={y∈E|d(x,y)=r}.{displaystyle S(x;r)={yin E|d(x,y)=r}.}

Una sfera in uno spazio metrico può essere un oggetto molto diverso dalla sfera usuale. Ad esempio, può essere vuota: se consideriamo Zn{displaystyle mathbb {Z} ^{n}} con la metrica euclidea, una sfera di raggio r{displaystyle r} è vuota se e solo se r2{displaystyle r^{2}} non può essere scritto come somma di n{displaystyle n} quadrati.

Formule |

Formule della Sfera
Circonferenza	U=2πr =dAPFdr{displaystyle U,=,2pi r{color {OliveGreen} ={frac {mathrm {d} A_{mathrm {PF} }}{mathrm {d} r}}}}
Superficie	AO=4πr2 =dVdr{displaystyle A_{O},=,4pi r^{2},{color {OliveGreen} ={frac {mathrm {d} V}{mathrm {d} r}}}}
Volume	V=43πr3=∫0rAOdr{displaystyle V,=,{frac {4}{3}}pi r^{3}=int _{0}^{r}A_{O}mathrm {d} r}
Area di un cerchio massimo	APF=πr2=∫0rUdr{displaystyle A_{mathrm {PF} },=,pi r^{2}=int _{0}^{r}Umathrm {d} r}
Volume di un segmento di sfera	VKS=h2π3(3r−h){displaystyle V_{mathrm {KS} },=,{frac {h^{2}pi }{3}}(3r-h)}
Area di una calotta sferica	AKK=2rhπ=2r2π(1−cos⁡α2){displaystyle A_{mathrm {KK} },=,2rhpi =2r^{2}pi left(1-cos {frac {alpha }{2}}right)}
Momento d'inerzia	J=25mr2{displaystyle J,=,{frac {2}{5}}mr^{2}}

Dove con r{displaystyle r} si intende il raggio della sfera, con h{displaystyle h} l'altezza del segmento di sfera o della calotta sferica, con α{displaystyle alpha } l'ampiezza in steradianti della calotta.Volume

Ingegneria |

.mw-parser-output .vedi-anche{border:1px solid #CCC;font-size:95%;margin-bottom:.5em}.mw-parser-output .vedi-anche td:first-child{padding:0 .5em}.mw-parser-output .vedi-anche td:last-child{width:100%}

Lo stesso argomento in dettaglio: Chilogrammo § Proposte per la definizione futura.

Per quanto si sia avvicinato, l'uomo non è ancora riuscito a produrre alcun oggetto dalla sfericità matematicamente perfetta. Finora il miglior risultato è stato raggiunto dall'Australian Centre for Precision Optics, di Lindfield (Australia). La sfera è stata ottenuta attraverso una levigazione ad altissima precisione di una barra di silicio 28 (un isotopo del silicio) ed è frutto del Progetto Avogadro, che si propone di arrivare alla definizione del chilogrammo perfetto, basata sulla conoscenza dell'esatto numero di atomi che compongono tale sfera^[1]. Il suo diametro è di 9,36 centimetri e come uniche imperfezioni presenta una rugosità di 0,3 nanometri e piccole deviazioni di sfericità di circa 60-70 nanometri. In precedenza, il miglior risultato era stato ottenuto dalla NASA, che per la sonda Gravity Probe B, costruita per degli studi gravitazionali in orbita, ha creato dei giroscopi con deviazioni inferiori ai 100 nanometri.

Filosofia |

Parmenide paragona l'Essere a una sfera perfetta, sempre uguale a se stessa nello spazio e nel tempo, chiusa e finita (per gli antichi greci il finito era sinonimo di perfezione). La sfera è infatti l'unico solido geometrico che non ha differenze al suo interno, ed è uguale dovunque la si guardi; l'ipotesi collima suggestivamente con la teoria della relatività di Albert Einstein che nel 1900 dirà:^[2] «Se prendessimo un binocolo e lo puntassimo nello spazio, vedremmo una linea curva chiusa all'infinito» in tutte le direzioni dello spazio, ovvero, complessivamente, una sfera (per lo scienziato infatti l'universo è finito sebbene illimitato, fatto di uno spazio tondo ripiegato su se stesso).^[3]

Note |

Voci correlate |

• Circonferenza


• Geometria sferica


• Trigonometria sferica


• Ipersfera


• Pseudosfera


• Palla (matematica)


• Sfera unitaria

Altri progetti |

• 
  Wikiquote contiene citazioni di o su sfera
  


• 
  Wikizionario contiene il lemma di dizionario «sfera»


• 
  Wikimedia Commons contiene immagini o altri file su sfera
  

Collegamenti esterni |

• 
  


• 
  Sfera, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
  

.mw-parser-output .navbox{border:1px solid #aaa;clear:both;margin:auto;padding:2px;width:100%}.mw-parser-output .navbox th{padding-left:1em;padding-right:1em;text-align:center}.mw-parser-output .navbox>tbody>tr:first-child>th{background:#ccf;font-size:90%;width:100%}.mw-parser-output .navbox_navbar{float:left;margin:0;padding:0 10px 0 0;text-align:left;width:6em}.mw-parser-output .navbox_title{font-size:110%}.mw-parser-output .navbox_abovebelow{background:#ddf;font-size:90%;font-weight:normal}.mw-parser-output .navbox_group{background:#ddf;font-size:90%;padding:0 10px;white-space:nowrap}.mw-parser-output .navbox_list{font-size:90%;width:100%}.mw-parser-output .navbox_odd{background:#fdfdfd}.mw-parser-output .navbox_even{background:#f7f7f7}.mw-parser-output .navbox_center{text-align:center}.mw-parser-output .navbox .navbox_image{padding-left:7px;vertical-align:middle;width:0}.mw-parser-output .navbox+.navbox{margin-top:-1px}.mw-parser-output .navbox .mw-collapsible-toggle{font-weight:normal;text-align:right;width:7em}.mw-parser-output .subnavbox{margin:-3px;width:100%}.mw-parser-output .subnavbox_group{background:#ddf;padding:0 10px}

V · D · M Topologia
Concetti di Topologia generale	Spazio topologico · Base · Prebase · Ricoprimento · Assiomi di chiusura di Kuratowski · Invariante topologico · Relazione di finezza · Partizione dell'unità · Proprietà dell'intersezione finita Sottoinsiemi Intervallo · Aperto · Intorno · Chiuso · Insieme localmente chiuso · Insieme chiuso-aperto · Parte interna · Chiusura · Frontiera · Insieme derivato · Insieme perfetto · Insieme denso · Insieme mai denso Punti Punto isolato · Punto di accumulazione · Punto di aderenza Funzioni Funzione continua · Omeomorfismo · Funzione aperta · Funzione chiusa · Funzione propria · Contrazione · Retrazione · Germe di funzione · Funzione a supporto compatto Successioni Limite · Limite di una successione · Successione · Rete · Convergenza · Successione di Cauchy Teoremi Teorema di Weierstrass · Heine-Borel · Tychonoff · Lemma del tubo · Urysohn · Tietze · Baire · Brouwer · punto fisso · Teorema di Borsuk · Teorema di Borsuk-Ulam · Teorema della curva di Jordan · Teorema della mappa di Riemann Applicazioni Topologia dello spazio-tempo · Topologia di rete · Controllo della topologia · Topologia molecolare
Proprietà	Numerabilità Assioma di numerabilità · Spazio primo-numerabile · Spazio separabile · Spazio sequenziale Separazione Assioma di separazione · Spazio T0 · Spazio T1 · Spazio di Hausdorff · Spazio regolare · Spazio di Tychonoff · Spazio normale Compattezza Spazio compatto · Spazio paracompatto · Spazio localmente compatto · Spazio di Lindelöf · Sottospazio relativamente compatto · Immersione compatta Connessione Spazio connesso · Spazio semplicemente connesso Metrizzabilità Spazio metrico · Spazio metrico completo · Spazio metrizzabile · Spazio ultrametrico · Spazio pseudometrico · Spazio polacco · Spazio normato · Spazio totalmente limitato Altro Spazio di Baire · Spazio topologico noetheriano · Spazio omogeneo
Spazi topologici	Topologie classiche Topologia banale · Spazio di Sierpiński · Cofinita · Topologia della semicontinuità inferiore · di Zariski · Euclidea · del limite inferiore o di Sorgenfrey · Discreta · Topologia degli interi equispaziati · Insieme reale esteso · Topologia di ordine · Piano di Moore Topologie indotte Topologia prodotto · Topologia di sottospazio · Topologia quoziente · Compattificazione (di Alexandrov · di Stone-Čech) · Cono · Bouquet · Sospensione Topologie in Analisi funzionale Topologia iniziale o debole · Topologia operatoriale · Topologia finale o forte · Topologia di Mackey · Topologia polare · Topologia operatoriale debole Altri oggetti topologici Sfera · Palla · Toro · Corpo con manici · Bottiglia di Klein · Bottiglia di Klein solida · Anello · Nastro di Möbius · Retta proiettiva · Piano proiettivo · Superficie di Riemann · Nodo · Link Frattali Insieme di Cantor · Spazio di Cantor · Polvere di Cantor · Sfera di Alexander · Curva di Peano Strutture miste Spazio vettoriale topologico · Gruppo topologico · Gruppo di Lie · Spazio uniforme · Algebra di Borel
Topologia algebrica	Gruppo fondamentale · Arco · Nerbo · Omotopia · Gruppi di omotopia · Omologia · Omologia singolare · Algebra omologica · Coomologia di De Rham · Spazio semplicemente connesso · Rivestimento · Grado topologico · Indice di avvolgimento · Sollevamento · Teorema del sollevamento dell'omotopia · Teorema di unicità del sollevamento · Teorema di Van Kampen · Caratteristica di Eulero · Formula di Eulero per i poliedri · Genere · Taglio · Numero di Betti · Superficie incompressibile · Successione di Mayer-Vietoris · Successione esatta · Successione spettrale · Teorema della palla pelosa · Schema simpliciale · Complesso simpliciale · Complesso di celle · Complesso di catene · Classificazione delle superfici · Mapping class group · Congettura di Hodge · Congettura di Poincaré
Topologia differenziale	Varietà · Varietà differenziabile · Varietà parallelizzabile · 3-varietà · 3-varietà irriducibile · Atlante · Diffeomorfismo · Diffeomorfismo locale · Diffeomorfismo di Anosov · Immersione · Curva · Superficie · Campo vettoriale · Fibrato · Fibrato principale · Fibrato vettoriale · Varietà fibrata · Fibrazione di Hopf · Varietà con bordo · Teorema dell'intorno tubolare · Teorema di Kneser-Milnor · Congettura di geometrizzazione di Thurston · Cobordismo · Dimensione topologica · Topologia in dimensione bassa · Chirurgia di Dehn · Trasversalità · Eversione della sfera · Teoria delle foliazioni

.mw-parser-output .CdA{border:1px solid #aaa;width:100%;margin:auto;font-size:90%;padding:2px}.mw-parser-output .CdA th{background-color:#ddddff;font-weight:bold;width:20%}

Controllo di autorità	GND (DE) 4165914-4

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica