Nsryjdtyk

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

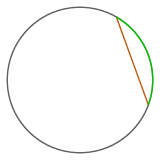
Un arco di circonferenza e la corda sottesa.

In geometria si definisce arco la parte di una curva regolare compresa fra due suoi punti, detti estremi dell'arco. Curve regolari sono le curve continue e dotate di tangente unica in ogni punto, come ad esempio quelle delle coniche.

Un arco può essere approssimato da una linea spezzata poligonale composta da un numero limitato di segmenti con i vertici disposti a intervalli regolari lungo l'arco stesso. Quando la lunghezza dei segmenti tende a zero, la lunghezza e l'andatura della poligonale tende a quella dell'arco.

Il segmento di retta delimitato dagli estremi di un arco si dice corda sottesa dall'arco. L'asse di tale segmento passa per il centro dell'arco.

Le misure degli archi di circonferenza sono espresse frequentemente in gradi o radianti, assumendo la circonferenza stessa, ovvero parte di essa, come unità di misura.

Per trovare la lunghezza l{displaystyle l} di un arco di circonferenza sotteso da due raggi r{displaystyle r} che formano un angolo θ{displaystyle theta } (espresso in radianti) fra loro si mettono in relazione, tramite proporzione, la lunghezza dell'arco con quella di tutta la circonferenza e l'angolo sotteso dai raggi con l'angolo giro:

 2π:θ=2πr:l{displaystyle 2pi :theta =2pi r:l}

e quindi la lunghezza dell'arco è

 l=θr{displaystyle l=theta r}

Voci correlate |

• Arco (architettura)


• Lunghezza di un arco


• Calotta sferica


• Teorema sugli archi congruenti

Altri progetti |

• 
  Wikimedia Commons contiene immagini o altri file su arco
  

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica