Nsryjdtyk

Illustrazione del 1547 di un esperimento sul principio di Archimede.

Il principio di Archimede afferma che «ogni corpo immerso parzialmente o completamente in un fluido (liquido o gas) riceve una spinta verticale dal basso verso l'alto, uguale per intensità al peso del volume del fluido spostato».

Generalità |

Il principio è così detto in onore di Archimede di Siracusa, matematico e fisico siracusano, vissuto nel III secolo a.C. che lo dimostrò nel primo libro della sua opera Sui corpi galleggianti. In realtà nell'opera, come ha giustamente sottolineato Lucio Russo,^[1] non è affermato alcun principio, ma quanto conosciuto come principio (proposizioni III - VII) è effettivamente dimostrabile soltanto considerando il postulato d'apertura che afferma (in sostanza) che due porzioni contigue di fluido non sono in equilibrio se diversamente compresse.

Dal postulato Archimede fa discendere le due prime proposizioni, rilevanti anch'esse in fisica perché (I proposizione) viene di fatto enunciato, anche se non è esplicitamente richiamato, il principio dei vasi comunicanti e (II proposizione) viene scientificamente dedotta per la prima volta la sfericità della Terra non basandosi su argomenti visivi come le eclissi o le navi che scompaiono all'orizzonte, bensì su dimostrazioni scientifiche: due punti delle acque della Terra, immaginata come una sola superficie liquida, non possono trovarsi a distanza diversa dal centro dei pesi (centro di gravità) dal momento che le colonne d'acqua, dall'estrema circonferenza terrestre al centro, si equivalgono in peso. La dimostrazione, solitamente trascurata dai testi che s'occupano delle prove della sfericità della Terra nel lontano passato, è rilevante per le conseguenze che implica. Ammettere la sfericità per il pianeta Terra vuol dire ammetterla per tutti i corpi celesti (i pianeti) osservati e considerati, passando così da una teoria geocentrica della gravità, aristiotelicamente confinata, ad una teoria policentrica della gravità.

Il cosiddetto principio di Archimede |

La classica formulazione delle dimostrazioni fornite da Archimede (Libro I, proposizioni III - VII) e note come “principio” è la seguente:

Tale forza è detta "forza di Archimede" o "spinta di Archimede" o ancora "spinta idrostatica" (nonostante non riguardi solo i corpi immersi in acqua, ma in qualunque altro fluido – liquido o gas). Una formulazione più semplice del principio è la seguente:

La spinta si applica al baricentro della massa di fluido spostata e non al baricentro della parte del corpo immersa nel fluido ed è diretta, secondo l'equazione fondamentale dell'idrostatica, verso il piano dei carichi idrostatici (o piano a pressione relativa nulla), che nella maggioranza dei casi coincide con il pelo libero del fluido, ed è quindi diretta verso l'alto. Archimede inventò la bilancia idrostatica, utilizzata per misurare il peso specifico dei liquidi. Sulla base di quelle rilevazioni, affermò:

Il principio è quindi un caso particolare dell'equazione fondamentale dell'idrostatica, che vale finché il fluido può essere trattato come un materiale continuo, e questo avviene solo fintanto che le dimensioni dei corpi immersi sono abbastanza grandi rispetto alle dimensioni delle molecole del fluido. Diversamente, il corpo (ad esempio dei granelli di polvere) è soggetto non più ad una spinta deterministica (di cui è noto modulo, direzione e verso, come quella di Archimede), ma ad una di carattere probabilistico che genera un moto browniano.

Nelle dimostrazioni Archimede non considera mai la forma del solido, si limita soltanto a specificarne le qualità: più leggero o più pesante del fluido. Solo all'VIII proposizione, ed alla successiva IX, Archimende inizia a considerare un <<segmento sferico>>, chiaro segno del passaggio alla più complessa tematica discussa nel libro II dove si occuperà delle condizioni di equilibrio e stabilità in un fluido di un conoide rettangolo (un paraboloide di rivoluzione). Alla proposizione VIII (libro I) è sinteticamente discusso il principio navale del metacentro e nel libro II è discussa di fatto la teoria della biforcazione

Cenni storici |

Questa voce o sezione sull'argomento scienza non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Rappresentazione dell'esperimento condotto da Archimede. Gerone II aveva commissionato ad un orefice una corona d'oro fornendogli per questo un certo quantitativo del prezioso metallo. (Questo non è probabilmente vero: Archimede avrebbe scoperto il principio di dislocamento che gli ha permesso di misurare il volume della corona, da cui la densità - vedi collegamenti esterni).

Col suo famoso «Eureka!» Archimede intendeva dire che "aveva trovato" la soluzione al problema postogli da Gerone II che gli aveva chiesto di aiutarlo a verificare uno sgradevole sospetto. Il sovrano, per celebrare un successo, aveva commissionato ad un orefice una corona d'oro fornendogli per questo un certo quantitativo del prezioso metallo. (Questo non è probabilmente vero: Archimede avrebbe scoperto il principio di dislocamento che gli ha permesso di misurare il volume della corona, da cui la densità - vedi collegamenti esterni).
A lavoro finito la corona pesava esattamente quanto l'oro fornito, ma aveva il dubbio che parte dell'oro fosse stata sostituita con un uguale peso di metallo più vile (argento o rame). Basandosi sulla sua intuizione, Archimede aveva capito che due materiali diversi, aventi lo stesso peso ma necessariamente due volumi diversi (es. un chilo di ferro ed un chilo di legno) ricevono diverse spinte se immersi nell'acqua e queste spinte dipendono esclusivamente dal volume e non dal tipo di materiale o dal suo peso. In particolare, data l'elevata densità dell'oro, il volume di una corona in metallo vile sarà maggiore e così la spinta.

Fu quindi sufficiente utilizzare una bilancia ed appendere la corona ad un braccio, e all'altro braccio un lingotto di oro puro con peso pari a quello della corona. La bilancia era ovviamente in equilibrio. I due oggetti vennero allora immersi in acqua alzando due recipienti posti uno sotto ogni braccio. La corona era in parte composta da metallo più vile che era stato aggiunto in ugual peso ma in maggior volume e quindi in totale la corona aveva maggior volume del lingotto d'oro. La corona riceveva pertanto una spinta maggiore e la bilancia si spostò dalla parte dell'oro denunciando la frode.

Leonardo da Vinci così spiegava il principio di Archimede quando propose la costruzione di un ponte canale per Milano a Ludovico il Moro: il gran peso della barca che passa per il fiume sostenuto dall'arco del ponte, non cresce peso a esso ponte, perché la barca pesa di punto quanto il peso dell'acqua che tal barca caccia dal suo sito.

Nel 2012 in uno studio condotto dal Politecnico di Milano e dall'Università degli Studi dell'Insubria-sede di Como, è stato mostrato sperimentalmente che il principio non sembra essere valido per dimensioni nanometriche venendo dunque meno il suo carattere di universalità.^[2]

Condizioni di equilibrio e non equilibrio di un corpo immerso |

Da un punto di vista matematico, la forza di Archimede può essere espressa nel modo seguente:

FA=ρflu g V{displaystyle F_{A}=rho _{flu} g V}

essendo ρ_flu la densità (massa volumica) del fluido, g l'accelerazione di gravità e V il volume spostato (che in questo caso è uguale al volume del corpo). Allo stesso modo, il peso del corpo è dato da

Fp=ρsol g V{displaystyle F_{p}=rho _{sol} g V}

essendo ρ_sol la densità media del solido immerso.

La spinta è indipendente dalla profondità alla quale si trova il corpo. La densità relativa (del corpo immerso nel fluido rispetto alla densità del fluido) è facilmente calcolabile senza misurare alcun volume:

Densità relativa in percentuale = Peso del corpo nello spazio vuotoPeso del corpo nello spazio vuoto −Peso della parte immersa nel fluido⋅100{displaystyle {frac {Peso del corpo nello spazio vuoto}{Peso del corpo nello spazio vuoto -Peso della parte immersa nel fluido}}cdot 100}

Il peso di un corpo immerso (parzialmente o totalmente) non è quello totale misurabile fuori dal liquido, ma il peso del volume di fluido spostato dalla parte immersa. Questa quantità riduce il peso del corpo (parte immersa e non nel fluido) quando si trova appeso ad un filo nello spazio vuoto.

Corpo immerso in un liquido |

Possono darsi tre casi (illustrati da sinistra a destra in figura):

• Il corpo tende a cadere fino a raggiungere il fondo se la forza di Archimede è minore del peso, F_A < F_p, ovvero se ρ_flu < ρ_sol.


• Il corpo si trova in una situazione di equilibrio se la forza di Archimede è uguale al peso, F_A = F_p, ovvero se ρ_flu = ρ_sol. Questo significa che se il corpo era in quiete rimarrà in quiete, mentre se era in moto si muoverà di moto decelerato fino a fermarsi per effetto dell'attrito.


• Il corpo tende a risalire fino alla superficie dove galleggia se la forza di Archimede è maggiore del peso, F_A > F_p, ovvero se ρ_flu > ρ_sol.

In questo caso il volume immerso V_i sarà tale da spostare un volume di fluido che equilibri il peso del corpo, ovvero:

ρflu g Vi=ρsol g V{displaystyle rho _{flu} g V_{i}=rho _{sol} g V}

da cui si deriva la formula del galleggiamento:

ViV=ρsolρflu{displaystyle {frac {V_{i}}{V}}={frac {rho _{sol}}{rho _{flu}}}}

La frazione di volume immerso è quindi uguale al rapporto tra le densità del corpo e del liquido. Nel caso di un iceberg che galleggia nel mare, la densità del ghiaccio è circa 917 kg/m³, mentre la densità dell'acqua salata è circa 1025 kg/m³; in base alla formula precedente, la percentuale di volume immerso è quindi dell'89,5%.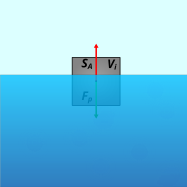

Dimostrazione della condizione di equilibrio nel galleggiamento |

Un corpo rigido è in una situazione di equilibrio se la risultante delle forze agenti su di esso e la risultante dei momenti delle forze sono nulli. Consideriamo un corpo rigido immerso in un liquido: esso assumerà una situazione di equilibrio se la risultante della forza peso e della forza di Archimede sarà nulla. La forza peso di un corpo è uguale a: Fp=mg{displaystyle Fp=mg} dove possiamo indicare la massa anche come prodotto tra densità e volume: Fp=ρfluVg{displaystyle Fp=rho _{flu}Vg} .Allo stesso modo anche la spinta di Archimede è uguale al prodotto tra la densità, il volume e l'accelerazione di gravità. Se il corpo è in equilibrio allora Fp=Fa{displaystyle Fp=Fa} quindi: ρfluVg=ρsolVg{displaystyle rho _{flu}Vg=rho _{sol}Vg}. Il corpo sarà in una situazione di galleggiamento, non si troverà né al di sopra, né al di sotto del liquido. A questo punto diremo quindi che il corpo avrà la stessa densità media del liquido in cui è immerso. Un esempio quotidiano è costituito, ad esempio, dai sommergibili. Ci chiediamo, infatti, perché a volte il sommergibile si trovi al di sopra del livello del mare e a volte scenda in profondità. Ciò avviene perché le stive del sommergibile vengono riempite di acqua marina nel caso in cui esso debba scendere in profondità, otterrà in questo modo circa la stessa densità dell'acqua. Quando dovrà salire a galla, le stive saranno riempite di aria compressa, in modo da eliminare l'acqua. Nel caso in cui si considerino corpi costituiti da densità differenti, si effettuerà la media delle densità, proprio come nel caso del sommergibile.

Corpo immerso nell'atmosfera (o in un altro gas) |

Le considerazioni fatte sopra per i liquidi valgono anche per i gas, con due importanti differenze:

• la densità dell'aria nell'atmosfera è oltre settecento volte minore di quella dell'acqua; questo fa sì che solo i corpi con densità molto bassa possono essere sollevati dalla spinta di Archimede;
  
  
  
  • la maggior parte dei corpi ha una densità maggiore di quella dell'aria e per questo cade;
  
  
  • alcuni corpi con densità uguale a quella dell'aria galleggiano;
  
  
  • i corpi con densità minore dell'aria vengono portati verso l'alto, come i palloncini di elio e le mongolfiere;
  
  
  
  


• a differenza dei liquidi, la densità nei gas non è costante, ma è funzione della pressione, secondo la seguente espressione, derivata dalla legge dei gas perfetti:

ρgas=pMRT{displaystyle rho _{gas}={frac {pM}{RT}}}

essendo p la pressione del gas, M la sua massa molecolare e T la sua temperatura assoluta, mentre R=8.314 J/mole K è la costante dei gas. Poiché nell'atmosfera, la pressione diminuisce con la quota, anche la densità dell'aria è una funzione decrescente della quota: ρ=ρ(z).
Una mongolfiera con ρ_flu < ρ_sol salirà fino ad una quota a cui la densità dell'aria calda interna è uguale a quella dell'aria esterna.

Generalizzazione |

Come la Legge di Stevino per i fluidi incomprimibili, anche la formulazione della spinta di Archimede può essere derivata dalla condizione di equilibrio idrostatico di un fluido ideale.

Esempi e applicazioni del principio di Archimede |

Questa voce o sezione sull'argomento scienza non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Il principio di Archimede vale per tutti i fluidi, siano essi liquidi o gas: una nave galleggia sull'acqua, ma anche una mongolfiera che sale verso l'alto sono dunque soggette allo stesso principio. Una nave, anche se di acciaio, essendo vuota (o meglio, piena d'aria), occupa un volume complessivo di materia (aria, acciaio, plastica, legno e quant'altro compone una nave) che ha un certo peso; siccome lo stesso volume di sola acqua ha un peso maggiore, la nave riceve una spinta verso l'alto che ne permette il galleggiamento; analogamente, una mongolfiera piena di aria calda o di elio (fluidi di peso specifico minore di quello dell'aria), risulta più leggera del volume di aria che sposta e viene spinta verso l'alto.^[3]

Un sommergibile in emersione ha una densità media minore di quella dell'acqua. Per potersi immergere deve aumentare la sua densità fino ad un valore maggiore di quello dell'acqua, allagando alcuni comparti interni. Per stabilizzarsi ad una certa profondità deve espellere una parte di quest'acqua in modo da raggiungere una densità pari a quella dell'acqua.^[4]

Diverse specie di pesci possono controllare in modo analogo il loro assetto subacqueo attraverso la vescica natatoria, che contiene aria. Comprimendo la vescica con l'azione dei muscoli riducono il volume d'aria incamerata, facendo diminuire l'intensità della spinta di Archimede e possono scendere; rilassando i muscoli la vescica si espande e possono invece risalire fino in superficie. Il subacqueo in immersione con autorespiratore effettua in pratica operazioni analoghe agendo sul proprio GAV.

La spinta di Archimede trova una sua applicazione nel fenomeno geo-fisico dell'isostasia, ovvero il fenomeno del "galleggiamento" della litosfera (rigida) sull'astenosfera (più fluida, in cui affondano le radici di un orogeno in formazione). La litosfera, attraverso assestamenti isostatici, tende poi a riportarsi in equilibrio con l'astenosfera con un procedimento analogo a quello del principio di Archimede finché non è finito il processo di formazione della nuova catena montuosa.

Note |

Bibliografia |

• Lucio Russo, La rivoluzione dimenticata, VII edizione, Milano, Feltrinelli, 2013, ISBN 9788807883231.

Voci correlate |

• Assetto (subacquea)


• Bilancia idrostatica


• Fluidodinamica


• Fluidostatica


• Idrodinamica


• Legge di Stevin


• Sostentamento idrodinamico

Altri progetti |

• 
  Wikiversità contiene lezioni su principio di Archimede
  


• 
  Wikimedia Commons contiene immagini o altri file su principio di Archimede
  

Collegamenti esterni |

• 
  


• 
  Principio di Archimede, su thes.bncf.firenze.sbn.it, Biblioteca Nazionale Centrale di Firenze.
  


• Animazione interattiva del principio di Archimede., su ww2.unime.it.


• (EN) Thermopedia, "Archimedes force", su thermopedia.com.


• http://www.scientificamerican.com/article/fact-or-fiction-archimede/

Portale Ellenismo

Portale Ingegneria

Portale Meccanica