Nsryjdtyk

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Raggio di un cerchio

Secondo la definizione classica della geometria, il raggio di un cerchio o di una sfera è un segmento di retta avente un estremo sulla circonferenza o superficie sferica e l'altro estremo nel centro della figura. Per estensione si definisce raggio di un cerchio o di una sfera anche la lunghezza di un tale segmento. Il raggio misura la metà del diametro.

Più generalmente — in geometria, ingegneria, teoria dei grafi, e in molti altri settori — il raggio di qualcosa (per esempio di un cilindro, di un grafo, o di un componente meccanico) è la distanza dei suoi punti più esterni dal centro o asse.

La definizione di raggio data per i cerchi e per le sfere si lascia estendere naturalmente al caso di iperspazi con più di tre dimensioni. Generalmente, un segmento che congiunge un punto di un'ipersfera al suo centro è un raggio dell'ipersfera.

In una spirale il raggio è una funzione dell'angolo. Tutte le circonferenze sono assimilabili a spirali con raggio costante.

Formule per i cerchi |

Raggio dal diametro |

Il raggio R{displaystyle R} di un cerchio avente diametro d{displaystyle d} è

R=d2.{displaystyle R={frac {d}{2}}.}

Raggio dalla circonferenza |

Il raggio R{displaystyle R} di un cerchio avente circonferenza C{displaystyle C} è

R=C2π.{displaystyle R={frac {C}{2pi }}.}

Raggio del cerchio |

Il raggio R{displaystyle R} di un cerchio avente area A{displaystyle A} è

R=Aπ.{displaystyle R={sqrt {frac {A}{pi }}}.}

Il raggio R{displaystyle R} della circonferenza che attraversa tre punti non collineari P1,P2,P3{displaystyle P_{1},P_{2},P_{3}} è dato da

R=|OP1→−OP3→|2sin⁡θ,{displaystyle R={frac {|{vec {OP_{1}}}-{vec {OP_{3}}}|}{2sin theta }},}

dove θ{displaystyle theta } è l'angolo ∠P1P2P3.{displaystyle angle P_{1}P_{2}P_{3}.} La formula è calcolata utilizzando il teorema dei seni.

Con riferimento alla figura a destra, lo stesso raggio R{displaystyle R} può anche essere espresso nel modo seguente:

R=a2sin⁡α,{displaystyle R={frac {a}{2sin alpha }},}

dove a{displaystyle a} indica la lunghezza del segmento di estremi B{displaystyle B} e C,{displaystyle C,} mentre α{displaystyle alpha } è l'angolo ∠BAC.{displaystyle angle BAC.}

Pertanto, se consideriamo tre punti di coordinate (x1,y1),(x2,y2){displaystyle (x_{1},y_{1}),(x_{2},y_{2})} e (x3,y3),{displaystyle (x_{3},y_{3}),} il raggio della circonferenza che li attraversa è dato da:

R=((x2−x1)2+(y2−y1)2)((x2−x3)2+(y2−y3)2)((x3−x1)2+(y3−y1)2)2|x1y2+x2y3+x3y1−x1y3−x2y1−x3y2|.{displaystyle R={frac {sqrt {((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})((x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2})((x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2})}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}|}}.}

Raggio dell'ellisse |

Lo stesso argomento in dettaglio: Ellisse.

Lo stesso argomento in dettaglio: Semiasse maggiore, Semiasse minore ed Eccentricità.

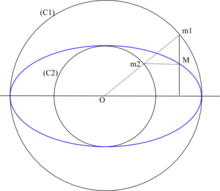
Il raggio medio R{displaystyle R} di un'ellisse è definito come il raggio di un cerchio di area (superficie) uguale a quella dell'ellisse.

È uguale alla radice quadrata del prodotto dei due semiassi dell'ellisse:

R=ab=a1−e24.{displaystyle R={sqrt {ab}}=a{sqrt[{4}]{1-e^{2}}}.}

Si definisce cerchio principale di un'ellisse, il cerchio con centro nel centro dell'ellisse e di raggio a,{displaystyle a,} uguale al semiassse maggiore dell'ellisse.

Si definisce cerchio secondario di un'ellisse, il cerchio con centro nel centro dell'ellisse e di raggio b,{displaystyle b,} uguale al semiasse minore dell'ellisse.

Raggio del poligono |

Il raggio di un poligono regolare è il segmento che unisce il centro a uno dei suoi vertici. Pertanto, la lunghezza di tale segmento è uguale al raggio della circonferenza circoscritta al poligono.

Il raggio R{displaystyle R} di un poligono di n{displaystyle n} lati di lunghezza an{displaystyle a_{n}} ciascuno, è dato da:

R=(an)22−2cos⁡(2π/n)=an2sin⁡(π/n).{displaystyle R={sqrt {frac {(a_{n})^{2}}{2-2cos(2pi /n)}}}={frac {a_{n}}{2sin(pi /n)}}.}

Il raggio in funzione della lunghezza dell'apotema h{displaystyle h}, è dato da:

R=hcos⁡(π/n).{displaystyle R={frac {h}{cos(pi /n)}}.}

Raccogliendo tutte le costanti (nella prima delle due formule), si può scrivere che il raggio R{displaystyle R} del poligono è R=R(an,n){displaystyle R=R(a_{n},n)}, ed è dato da R=rnan,{displaystyle R=r_{n}a_{n},} con rn=1/(2sin⁡πn).{displaystyle r_{n}=1/left(2sin {frac {pi }{n}}right).}

Si arriva così alla tabella dei seguenti numeri fissi:

nrnnrn20,50000000101,6180340−30,5773503−111,7747328−40,7071068−121,9318517−50,8506508+132,0892907+61,00000000142,2469796+71,1523824+152,4048672−81,3065630−162,5629154+91,4619022+172,7210956−{displaystyle {begin{array}{r|ccr|c}n&r_{n}&&n&r_{n}\hline 2&0,50000000&&10&1,6180340-\3&0,5773503-&&11&1,7747328-\4&0,7071068-&&12&1,9318517-\5&0,8506508+&&13&2,0892907+\6&1,00000000&&14&2,2469796+\7&1,1523824+&&15&2,4048672-\8&1,3065630-&&16&2,5629154+\9&1,4619022+&&17&2,7210956-end{array}}}

che, noti la lunghezza e il numero di lati, permette di calcolare il raggio del poligono.

Raggio di un ipercubo |

Il raggio R{displaystyle R} di un ipercubo d{displaystyle d}-dimensionale e lato an{displaystyle a_{n}}, è:

R=an2d.{displaystyle R={frac {a_{n}}{2}}{sqrt {d}}.}

Voci correlate |

• Raggio terrestre


• Curvatura

Altri progetti |

• 
  Wikizionario contiene il lemma di dizionario «raggio»


• 
  Wikimedia Commons contiene immagini o altri file su raggio
  

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica